高中数学空间向量的应用试题

在边长为的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合于B，构成一个三棱锥(如图所示)．

（Ⅰ）在三棱锥上标注出、点，并判别MN与平面AEF的位置关系，并给出证明；
（Ⅱ）是线段上一点，且,问是否存在点使得,若存在，求出的值;若不存在，请说明理由；
（Ⅲ）求多面体E-AFNM的体积．

点P在正方体的面对角线上运动，则下列四个命题：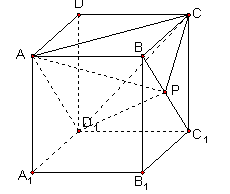

①三棱锥的体积不变；
②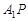∥平面；
③；
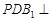④平面平面.
其中正确的命题序号是             .

已知是两条不同的直线，是三个不同的平面，下列命题正确的是(    )

A．若，则．

B．若，则．

C．若，则．

D．若，则．

已知α，β，γ是三个不同的平面，α∩γ＝m，β∩γ＝n．则（   ）

A．若m⊥n，则α⊥β	B．若α⊥β，则m⊥n
C．若m∥n，则α∥β	D．若α∥β，则m∥n

如图，已知在侧棱垂直于底面的三棱柱中，,且，点是中点．

(1)求证：平面⊥平面；
(2)若直线与平面所成角的正弦值为，
求三棱锥的体积．

设和是两个不重合的平面，给出下列命题：
①若外一条直线与内一条直线平行，则；
②若内两条相交直线分别平行于内的两条直线 ，则；
③设，若内有一条直线垂直于，则；
④若直线与平面内的无数条直线垂直,则.
上面的命题中，真命题的序号是 （ 　　 ）

A．①③

B．②④

C．①②

D．③④

如图，四棱柱的底面是平行四边形，且底面，，，°，点为中点，点为中点.

（Ⅰ）求证：平面平面；
（Ⅱ）设二面角的大小为，直线与平面所成的角为，求的值.

如图，已知四棱锥P-ABCD的底面为直角梯形，AD∥BC，∠BCD=90⁰，PA=PB，PC=PD.

(I) 试判断直线CD与平面PAD是否垂直，并简述理由；
（II）求证：平面PAB⊥平面ABCD；
（III）如果CD=AD+BC，二面角P-CB-A等于60⁰，求二面角P-CD-A的大小.

某个实心零部件的形状是如下图所示的几何体，其下部是底面均是正方形，侧面是全等的等腰梯形的四棱台，上部是一个底面与四棱台的上底面重合，侧面是全等的矩形的四棱柱.

（1）证明：直线平面；
（2）现需要对该零部件表面进行防腐处理.已知，，，（单位：），每平方厘米的加工处理费为元，需加工处理费多少元？

如图,正方体中，点在侧面及其边界上运动，并且总是保持，则动点的轨迹是     （   ）

A．线段

B．线段

C．中点与中点连成的线段

D．中点与中点连成的线段

给出下列关于互不相同的直线和平面的四个命题：
①若，，点，则与不共面；
②若、是异面直线，，，且，，则；
③若，则；
④若，，，，，则.
其中为假命题的是（   ）

A．①

B．②

C．④

D．③

给出下列关于互不相同的直线和平面的四个命题：
①若，，点，则与不共面；
②若、是异面直线，，，且，，则；
③若，则；
④若，，，，，则.
其中为假命题的是（   ）

A．①

B．②

C．④

D．③

三棱锥P−ABC中，PA⊥平面ABC，AB⊥BC。

（１）证明：平面PAB⊥平面PBC；
（２）若PA=，PC与侧面APB所成角的余弦值为，PB与底面ABC成60°角，求二面角B―PC―A的大小。

（本小题满分14分）如图，在四面体A−BCD中，AD^平面BCD，BC^CD，AD=2，BD=2．M是AD的中点.

（1）证明：平面ABC平面ADC；
（2）若ÐBDC=60°，求二面角C−BM−D的大小．

如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=，PA=，∠ABC=120°，G为线段PC的中点.

（1）证明：PA//平面BGD；
（2）求直线DG与平面PAC所成的角的正切值.