设 和
和 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于 内的两条直线,则
内的两条直线,则 平行于
平行于 ;
;
(2)若 外一条直线
外一条直线 与
与 内的一条直线平行,则
内的一条直线平行,则 和
和 平行;
平行;
(3)设 和
和 相交于直线
相交于直线 ,若
,若 内有一条直线垂直于
内有一条直线垂直于 ,则
,则 和
和 垂直;
垂直;
(4)直线 与
与 垂直的充分必要条件是
垂直的充分必要条件是 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
如图,已知DE⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。
平行四边形 中,
中, ,
, ,
, ,以
,以 为折线,把
为折线,把 折起,使平面
折起,使平面 平面
平面 ,连结
,连结 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的大小.
的大小.
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中, 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)求证:EM∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面 ? 若存在,确定
? 若存在,确定
点N的位置;若不存在,请说明理由.
如图,在三棱锥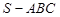 中,侧面
中,侧面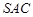 与底面
与底面 垂直,
垂直, 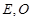 分别是
分别是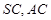 的中点,
的中点,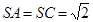
 ,
,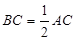 ,
,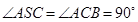 .
.
(1)若点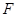 在线段
在线段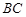 上,问:无论
上,问:无论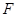 在
在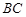 的何处,是否都有
的何处,是否都有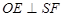 ?请证明你的结论;
?请证明你的结论;
(2)求二面角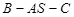 的平面角的余弦.
的平面角的余弦.
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有 ( )
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900.
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
在底面为正方形的长方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号)
①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.
试题篮
()