(本小题满分14分)如图5,正△ 的边长为4,
的边长为4, 是
是 边上的高,
边上的高, 分别是
分别是 和
和 边的中点,现将△
边的中点,现将△ 沿
沿 翻折成直二面角
翻折成直二面角 .
.
(1)试判断直线 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角 的余弦值;
的余弦值;
(3)在线段 上是否存在一点
上是否存在一点 ,使
,使 ?如果存在,求出
?如果存在,求出 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
(本小题满分14分)
如图①边长为1的正方形ABCD中,点E、F分别
为AB、BC的中点,将△BEF剪去,将
△AED、△DCF分别沿DE、DF折起,使A、
C两点重合于点P得一个三棱锥如图②示.
(1)求证: ;
;
(2)求三棱锥 的体积;
的体积;
(3)求DE与平面PDF所成角的正弦值. 

.如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD= .
.
(1)求四棱锥S-ABCD的体积;
(2)求证:面SAB⊥面SBC;
(3)求二面角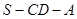 的正切值.
的正切值.
(本题共10分)
将两块三角板按图甲方式拼好,其中 ,
, ,
, ,
, ,现将三角板
,现将三角板 沿
沿 折起,使
折起,使 在平面
在平面 上的射影恰好在
上的射影恰好在 上,如图乙.
上,如图乙.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(本小题满分12分)
已知 是矩形,
是矩形,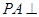 平面
平面 ,
, ,
, ,
,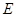 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成的角.
所成的角.
(本小题满分14分)
如图,在四棱锥 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形, 与
与 的交点为
的交点为 ,
, 为侧棱
为侧棱 上一点.
上一点.
(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC
(本小题满分12分)
如图,已知 ,
, 分别是正方形
分别是正方形 边
边 、
、 的中点,
的中点, 与
与 交于点
交于点 ,
, 、
、 都垂直于平面
都垂直于平面 ,且
,且 ,
,  ,
, 是线段
是线段 上一动点.
上一动点.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)试确定点 的位置,使得
的位置,使得 平面
平面 ;
;
(Ⅲ)当 是
是 中点时,求二面角
中点时,求二面角 的余弦值.
的余弦值.
如图1,在边长为 的正三角形
的正三角形 中,
中, ,
, ,
, 分别为
分别为 ,
, ,
, 上的点,且满足
上的点,且满足 .将△
.将△ 沿
沿 折起到△
折起到△ 的位置,使二面角
的位置,使二面角 成直二面角,连结
成直二面角,连结 ,
, .(如图2)
.(如图2)

(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的大小.
所成角的大小.
如图,在四棱锥P-ABCD中,PA 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:CD 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于 ,求k的取值范围.
,求k的取值范围.
(本小题满分12分)
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA^CD,PA = 1, PD=,E为PD上一点,PE = 2ED.

(Ⅰ)求证:PA^平面ABCD;
(Ⅱ)求二面角D-AC-E的余弦值;
(Ⅲ)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.
(本小题满分12分)如图,在三棱锥 中,底面
中,底面 是边长为4的正三角形,平面
是边长为4的正三角形,平面
 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
(1)求证:
(2)求二面角 的余弦值.
的余弦值.
(本小题满分14分)
如图,四棱锥 中,
中, 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面 平面
平面 ,
, ,
, .
.
(Ⅰ) 若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(II)试问点 在线段
在线段 上什么位置时,二面角
上什么位置时,二面角 的余弦值为
的余弦值为 .
.
如图,三棱柱ABC—A1B1C1中,AA1 面ABC,BC
面ABC,BC AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。
(1)若AA1=2,求证: ;
;
(2)若AA1=3,求二面角C1—BD—C的余弦值.
试题篮
()