已知四棱锥 中,底面ABCD为
中,底面ABCD为 的菱形,
的菱形, 平面ABCD,点Q在直线PA上.
平面ABCD,点Q在直线PA上.
(Ⅰ)证明:直线QC 直线BD;
直线BD;
(Ⅱ)若二面角 的大小为
的大小为 ,点M为BC的中点,求直线QM与AB所成角的余弦值.
,点M为BC的中点,求直线QM与AB所成角的余弦值.
(本小题满分12分)如图,在四棱锥 中,
中, 底面
底面 ,
, 是直角梯形,
是直角梯形, ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)求证;平面 平面
平面 ;
;
(2)若二面角 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)如图1,在边长为 的正方形
的正方形 中,
中, ,且
,且 ,且
,且 ,
, 分别交
分别交 于点
于点 ,将该正方形沿
,将该正方形沿 折叠,使得
折叠,使得 与
与 重合,构成图
重合,构成图 所示的三棱柱
所示的三棱柱 ,在图
,在图 中:
中:
(1)求证: ;
;
(2)在底边 上有一点
上有一点 ,使得
,使得 平面
平面 ,求点
,求点 到平面
到平面 的距离.
的距离.
如图,已知四棱锥S-A BCD是由直角梯形沿着CD折叠而成,其中SD=DA=AB=BC=l,AS∥BC,A⊥AD,且二面角S-CD-A的大小为120o.
(Ⅰ)求证:平面ASD⊥平面ABCD;
(Ⅱ)设侧棱SC和底面ABCD所成角为 ,求
,求 的正弦值.
的正弦值.
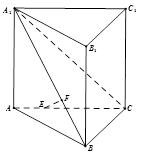
如图,在直三棱柱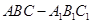 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面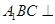 侧面
侧面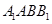 ,
,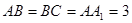 ,线段AC、A1B上分别有一点E、F且满足
,线段AC、A1B上分别有一点E、F且满足 .
.
(1)求证: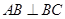 ;
;
(2)求点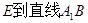 的距离;
的距离;
(3)求二面角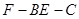 的平面角的余弦值。
的平面角的余弦值。
如图,三棱锥P-ABC中,E,D分别是棱BC,AC的中点,PB="PC=AB=4,AC=8," BC= ,PA=
,PA= .
.
(Ⅰ)求证:BC⊥平面PED;
(Ⅱ)求直线AC与平面PBC所成角的正弦值.
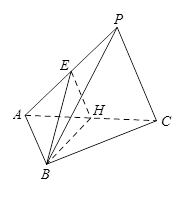
如图,在三棱锥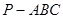 中,△
中,△ 是边长为
是边长为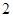 的正三角形,
的正三角形,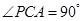 ,
, 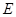 ,
,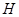 分别为
分别为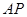 ,
,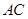 的中点,
的中点,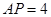 ,
,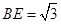 .
. 
(Ⅰ)求证: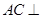 平面
平面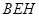 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,在正四棱台 中,
中, ,
, ,
, ,
, 、
、 分别是
分别是 、
、 的中点.
的中点. 
(Ⅰ)求证:平面 ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 .
.
注:底面为正方形,从顶点向底面作垂线,垂足是底面中心,这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥,底面与截面之间的部分叫做正四棱台.
(本小题满分14分)
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.

(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
⑴求证:PA∥平面BDE;
⑵求证:平面BDE⊥平面PBC.
(本小题满分12分)
如图,已知 ,
, 分别是正方形
分别是正方形 边
边 ,
, 的中点,
的中点, 与
与 交于点
交于点 ,
, 都垂直于平面
都垂直于平面 ,且
,且 ,
, 是
是 中点.
中点.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
试题篮
()