 是两个不同的平面,
是两个不同的平面, 是平面
是平面 及
及 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断:
① ②
② ③
③ ④
④ 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
在梯形ABCD中,AB∥CD,AB 平面α,CD
平面α,CD 平面α,则直线CD与平面α内的直线的位置关系可能是________.
平面α,则直线CD与平面α内的直线的位置关系可能是________.
在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为________________.
已知平面α,β,直线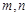 .给出下列命题:
.给出下列命题:
① 若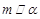 ,
, ,则
,则 ;
;
② 若 ,
, ,则
,则 ;
;
③ 若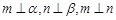 ,则
,则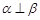 ;
;
④ 若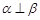 ,
,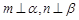 ,则
,则 .
.
其中是真命题的是 .(填写所有真命题的序号).
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
①直线BE与直线CF异面;
②直线BE与直线AF异面;
③直线EF∥平面PBC;
④平面BCE⊥平面PAD.
其中正确的有__________.
如图,在直角梯形ABCD中, ,M、N分别是AD、BE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
,M、N分别是AD、BE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
①不论D折至何位置(不在平面ABC内)都有 ;
;
②不论D折至何位置都有 ;
;
③不论D折至何位置(不在平面ABC内)都有 ;
;
④在折起过程中,一定存在某个位置,使 。
。
如图所示, 为正方体,给出以下五个结论:
为正方体,给出以下五个结论:
① 平面
平面 ;
;
② ⊥平面
⊥平面 ;
;
③ 与底面
与底面 所成角的正切值是
所成角的正切值是 ;
;
④二面角 的正切值是
的正切值是 ;
;
⑤过点 且与异面直线
且与异面直线 和
和  均成70°角的直线有2条.
均成70°角的直线有2条.
其中,所有正确结论的序号为________.
若 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线 ,则在平面
,则在平面 内,一定不存在与直线
内,一定不存在与直线 平行的直线.
平行的直线.
②若直线 ,则在平面
,则在平面 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线 垂直.
垂直.
③若直线 ,则在平面
,则在平面 内,不一定存在与直线
内,不一定存在与直线 垂直的直线.
垂直的直线.
④若直线 ,则在平面
,则在平面 内,一定存在与直线
内,一定存在与直线 垂直的直线.
垂直的直线.
已知直线l⊥平面α,直线m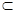 平面β,有下列四个命题:①若α∥β,则l⊥m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
平面β,有下列四个命题:①若α∥β,则l⊥m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
 是异面直线,下面四个命题:
是异面直线,下面四个命题:
①过 至少有一个平面平行于
至少有一个平面平行于 ;
;
②过 至少有一个平面垂直于
至少有一个平面垂直于 ;
;
③至多有一条直线与 都垂直;
都垂直;
④至少有一个平面与 都平行.
都平行.
其中正确命题的个数是
如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为 ,则
,则 的最大值为 .
的最大值为 .

如图,长方体 中,
中, 是边长为
是边长为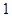 的正方形,
的正方形, 与平面
与平面 所成的角为
所成的角为 ,则棱
,则棱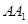 的长为_______;二面角
的长为_______;二面角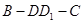 的大小为_______.
的大小为_______.
已知正方体 ,点
,点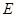 、
、 、
、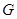 分别是棱
分别是棱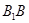 、
、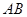 和
和 上的动点,观察直线
上的动点,观察直线 与
与 ,
, 与
与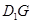 .
.
给出下列结论:
①对于任意点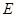 ,存在点
,存在点 ,使得
,使得
 ;②对于任意点
;②对于任意点 ,存在点
,存在点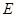 ,使得
,使得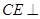
 ;
;
③对于任意点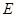 ,存在点
,存在点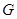 ,使得
,使得
 ;④对于任意点
;④对于任意点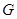 ,存在点
,存在点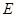 ,使得
,使得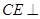
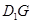 .
.
其中,所有正确结论的序号是__________.
试题篮
()