已知 过定点
过定点 ,圆心
,圆心 在抛物线
在抛物线 :
: 上运动,
上运动, 为圆
为圆 在
在 轴上所截得的弦.
轴上所截得的弦.
⑴当 点运动时,
点运动时, 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;
⑵当 是
是 与
与 的等差中项时,
的等差中项时,
试判断抛物线 的准线与圆
的准线与圆 的位置关系,
的位置关系,
并说明理由。
如图, 所在的平面
所在的平面 和四边形
和四边形 所在的平面
所在的平面 垂直,且
垂直,且 ,
, ,
, ,
, ,
, ,则点
,则点 在平面
在平面 内的轨迹是 ( )
内的轨迹是 ( )
| A.圆的一部分 |
| B.椭圆的一部分 |
| C.双曲线的一部分 |
| D.抛物线的一部分 |

已知椭圆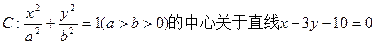 的对称点落在直线
的对称点落在直线 )上,且椭圆C的离心率为
)上,且椭圆C的离心率为
(1)求椭圆C的方程;
(2)设A(3,0),M、N是椭圆C上关于x轴对称的任意两点,连结AN交椭圆于另一点E,求证直线ME与x轴相交于定点.
)
已知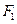 、
、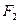 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为坐标原点,点
为坐标原点,点 在椭圆上,线段
在椭圆上,线段 与
与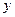 轴的交点
轴的交点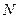 满足
满足 ;
;
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右焦点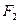 作直线l交椭圆于A、B两点,交y轴于M点,若
作直线l交椭圆于A、B两点,交y轴于M点,若 ,求
,求 的值.
的值.
在平面直角坐标系中,两点间的"
距离"定义为
则平面内与
轴上两个不同的定点
的"
距离"之和等于定值(大于
)的点的轨迹可以是()
| A. |
|
B. |
|
| C. |
|
D. |
|
已知双曲线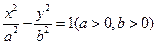 的一条渐近线方程是y=
的一条渐近线方程是y=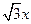 ,它的一个焦点在抛物线
,它的一个焦点在抛物线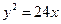 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为
A.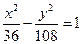 |
B.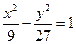  |
C.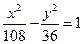 |
D.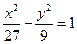 |
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点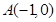 、
、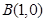 ,点
,点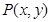 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点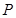 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到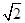 倍后得到点
倍后得到点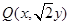 满足
满足 .
.
(1) 求动点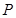 所在曲线
所在曲线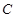 的轨迹方程;
的轨迹方程;
(2)(理科)过点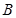 作斜率为
作斜率为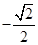 的直线
的直线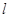 交曲线
交曲线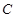 于
于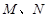 两点,且满足
两点,且满足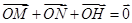 ,又点
,又点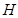 关于原点O的对称点为点
关于原点O的对称点为点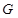 ,试问四点
,试问四点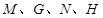 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点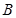 作斜率为
作斜率为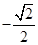 的直线
的直线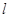 交曲线
交曲线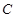 于
于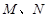 两点,且满足
两点,且满足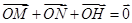 (O为坐标原点),试判断点
(O为坐标原点),试判断点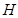 是否在曲线
是否在曲线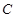 上,并说明理由.
上,并说明理由.
在平面直角坐标系中,O为坐标原点,给定两点A(1,0),B(0,—2),点C满足 ,其中
,其中 ,且
,且 ,
,
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线 (a>0,b>0)相交于M、N两点,且以MN为直径的圆经过原点,求证:
(a>0,b>0)相交于M、N两点,且以MN为直径的圆经过原点,求证: 为定值;
为定值;
(3)在(2)的条件下,若双曲线的离心率不大于 ,求双曲线实轴长的取值范围。
,求双曲线实轴长的取值范围。
试题篮
()