如图,动点M与两定点A(-1,0),B(2,0)构成△MAB,且∠MBA=2∠MAB.设动点M的轨迹为C.
(1)求轨迹C的方程;
(2)设直线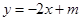 (其中
(其中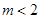 )与y轴相交于点P,与轨迹C相交于点Q,R,且
)与y轴相交于点P,与轨迹C相交于点Q,R,且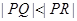 ,求
,求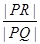 的取值范围.
的取值范围.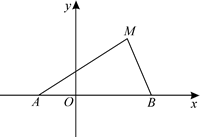
在平面直角坐标系中,O为坐标原点,给定两点A(1,0),B(0,—2),点C满足 ,其中
,其中 ,且
,且 ,
,
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线 (a>0,b>0)相交于M、N两点,且以MN为直径的圆经过原点,求证:
(a>0,b>0)相交于M、N两点,且以MN为直径的圆经过原点,求证: 为定值;
为定值;
(3)在(2)的条件下,若双曲线的离心率不大于 ,求双曲线实轴长的取值范围。
,求双曲线实轴长的取值范围。
(本小题满分15分)已知椭圆 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C,
上顶点为B,过F,B,C三点作 ,其中圆心P的坐标为
,其中圆心P的坐标为 .
.
(1) 若椭圆的离心率 ,求
,求 的方程;
的方程;
(2)若 的圆心在直线
的圆心在直线 上,求椭圆的方程.
上,求椭圆的方程.
四、选考题(本小题满分10分)
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
22.选修4-1:几何证明选讲
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
(1)求证:  ;
;
(2)若AC=3,求 的值。
的值。
(本小题满分12分)
已知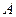 、
、 分别是直线
分别是直线 和
和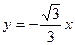 上的两个动点,线段
上的两个动点,线段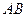 的长为
的长为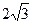 ,
, 是
是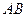 的中点.
的中点.
(1)求动点 的轨迹
的轨迹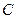 的方程;
的方程;
(2)过点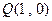 作直线
作直线 (与
(与 轴不垂直)与轨迹
轴不垂直)与轨迹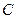 交于
交于 两点,与
两点,与 轴交于点
轴交于点 .若
.若 ,
, ,证明:
,证明: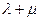 为定值.
为定值.
如图,已知椭圆的中心在坐标原点,焦点在 轴上,它的一个顶点为
轴上,它的一个顶点为 ,且离心率等于
,且离心率等于 ,过点
,过点 的直线
的直线 与椭圆相交于不同两点
与椭圆相交于不同两点 ,点
,点 在线段
在线段 上。
上。
(1)求椭圆的标准方程;
(2)设 ,若直线
,若直线 与
与 轴不重合,
轴不重合,
试求 的取值范围。
的取值范围。
:如图所示,AC和AB分别是圆O的切线,B、C为切点, 且OC = 3,AB = 4,延长OA到D点,则△ABD的面积是___________.
且OC = 3,AB = 4,延长OA到D点,则△ABD的面积是___________.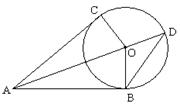

如右图,在平面直角坐标系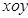 中,已知“葫芦”曲线
中,已知“葫芦”曲线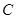 由圆弧
由圆弧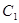 与圆弧
与圆弧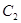 相接而成,两相接点
相接而成,两相接点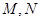 均在直线
均在直线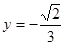 上.圆弧
上.圆弧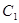 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点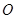 ,半径为
,半径为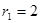 ;圆弧
;圆弧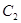 过点
过点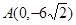 .
.
(I)求圆弧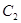 的方程;
的方程;
(II)已知直线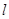 :
: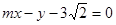 与“葫芦”曲线
与“葫芦”曲线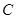 交于
交于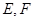 两点.当
两点.当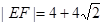 时,求直线
时,求直线 的方程.
的方程.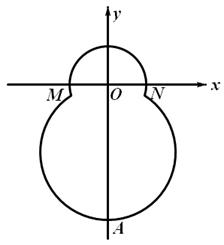
如图,椭圆
的一个焦点是
,
为坐标原点。
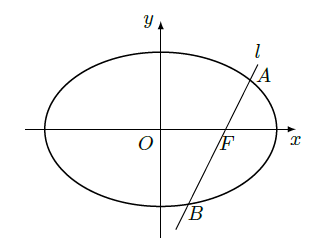
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点
的直线
交椭圆于
、
两点,若直线
绕点
任意转动,值有
,求
的取值范围。
试题篮
()