高中数学二次剩余试题

. 已知函数，其中，
(1)当时，把函数写成分段函数的形式；
(2)当时，求在区间[1,3]上的最值；
(3)设，函数在(m,n)上既有最大值又有最小值，请分别求出m,n的取值范围
（用表示）．

若x≥0，y≥0，且，则的最小值是          。

（本小题满分14分）
已知二次函数的图象过点，且函数对称轴方程为.
（Ⅰ）求函数的解析式；
（Ⅱ）设函数，求在区间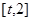上的最小值；
（Ⅲ）探究：函数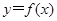的图象上是否存在这样的点，使它的横坐标是正整数，纵坐标是一个完全平方数？如果存在，求出这样的点的坐标；如果不存在，请说明理由.

设，若，且，则的取值范围是        （     ）

A．

B．

C．

D．

设二次函数f(x)＝ax²－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是(　　)

A．(－∞，0]	B．[2，＋∞)
C．(－∞，0]∪[2，＋∞)	D．[0,2]

函数图像上的动点到直线的距离为，点到轴的距离为，则的值为                                                    （    ）

A．

B．

C．

D．不确定的正数

已知为常数，函数在区间上的最大值为，则实数的值为_____________．

设，一元二次方程有整数根的充要条件是____________．

若函数在区间上存在反函数，则实数的取值范围是_______．

已知函数，，对于任意的都能找到，使得，则实数的取值范围是              ．

已知函数的定义域为，值域为，试确定这样的集合最多有       个

、已知函数在定义域内是增函数，则实数的取值范围( 　)

A．

B．

C．

D．

如果函数=x+2(a-1)x+2在区间(－∞，4)上是减函数，则实数a的取值范围是（   ）。

A．a≥－3

B． a≤－3

C． a≤5

D． a≥3

已知函数，，它在上单调递减，则的取值范围是　　　  （   ）

A．

B．

C．

D．