高中数学第二数学归纳法试题

已知f(n)=1+++…+(n∈N^*),用数学归纳法证明f(2ⁿ)>时,f(2^k+1)-f(2^k)等于　　　.

已知多项式f(n)＝n⁵＋n⁴＋n³－n.
(1)求f(－1)及f(2)的值；
(2)试探求对一切整数n，f(n)是否一定是整数？并证明你的结论．

2013年我国汽车拥有量已超过2亿（目前只有中国和美国超过2亿），为了控制汽车尾气对环境的污染，国家鼓励和补贴购买小排量汽车的消费者，同时在部分地区采取对新车限量上号.某市采取对新车限量上号政策，已知2013年年初汽车拥有量为（=100万辆），第年（2013年为第1年，2014年为第2年，依次类推）年初的拥有量记为，该年的增长量和与的乘积成正比，比例系数为其中=200万.
（1）证明：；
（2）用表示；并说明该市汽车总拥有量是否能控制在200万辆内.

用数学归纳法证明：（n+1）+（n+2）+…+（n+n）=的第二步中，当n=k+1时等式左边与n=k时的等式左边的差等于             .

在应用数学归纳法证明凸n变形的对角线为条时，第一步检验n等于（　）

A．1

B．2

C．3

D．0

（本小题满分15分）已知函数．
（1）当时，求在最小值；
（2）若存在单调递减区间，求的取值范围；
（3）求证：（）．

数列的前项组成集合，从集合中任取个数，其所有可能的个数的乘积的和为（若只取一个数，规定乘积为此数本身），记．例如：当时，，，；当时，，，．
（Ⅰ）求；
（Ⅱ）猜想，并用数学归纳法证明．

数列的前项组成集合，从集合中任取个数，其所有可能的个数的乘积的和为（若只取一个数，规定乘积为此数本身），记．例如：当时，，，；当时，，，．
（Ⅰ）求；
（Ⅱ）猜想，并用数学归纳法证明．

如图，在圆内：画1条弦，把圆分成2部分；画2条相交的弦，把圆分成4部分，画3条两两相交的弦，把圆最多分成7部分；…，画条两两相交的弦，把圆最多分成            部分.

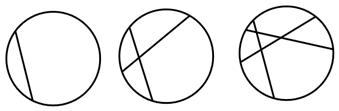
已知函数
（Ⅰ）若函数在其定义域上为单调函数,求的取值范围；
（Ⅱ）若函数的图像在处的切线的斜率为0，，已知求证：
（Ⅲ）在（2）的条件下，试比较与的大小，并说明理由.      

设是定义在正整数集上的函数,且满足：“当成立时，总可推出成立”，那么，下列命题总成立的是 （  ）

A．若成立，则成立

B．若成立，则当时，均有成立

C．若成立，则成立

D．若成立，则当时，均有成立

用数学归纳法证明（），在验证当n=1时，等式左边应为

A．1

B．1+a

C．1+a+a^2

D．1+a+a^2+a^3

设且，证明：
．

用数学归纳法证明不等式，第二步由k到k+1时不等式左边需增加（      ）

A．	B．
C．	D．

用数学归纳法证明等式时，第一步验证时，左边应取的项是

A．1

B．

C．

D．