如图,游客在景点 处下山至
处下山至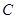 处有两条路径.一条是从
处有两条路径.一条是从 沿直道步行到
沿直道步行到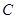 ,另一条是先从
,另一条是先从 沿索道乘缆车到
沿索道乘缆车到 ,然后从
,然后从 沿直道步行到
沿直道步行到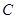 .现有甲、乙两位游客从
.现有甲、乙两位游客从 处下山,甲沿
处下山,甲沿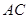 匀速步行,速度为
匀速步行,速度为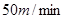 .在甲出发
.在甲出发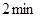 后,乙从
后,乙从 乘缆车到
乘缆车到 ,在
,在 处停留
处停留 后,再从
后,再从 匀速步行到
匀速步行到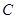 .假设缆车匀速直线运动的速度为
.假设缆车匀速直线运动的速度为 ,索道
,索道 长为
长为 ,经测量
,经测量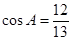 ,
, .
.
(1)求山路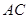 的长;
的长;
(2)假设乙先到,为使乙在 处等待甲的时间不超过
处等待甲的时间不超过 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
已知函数f(x)=sinx+cosx,f′(x)是f(x)的导函数,F(x)=f(x)f′(x)+f2(x)
(Ⅰ)求F(x)的最小正周期及单调区间;
(Ⅱ)求函数F(x)在 上的值域;
上的值域;
(Ⅲ)若f(x)=2f′(x),求 的值.
的值.
已知函数 ,若
,若 的最大值为1
的最大值为1
(Ⅰ)求 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,角
中,角 、
、 、
、 的对边
的对边 、
、 、
、 ,若
,若 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.
试题篮
()