如图,在 中, , , 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 , .
(1)比较 与 的大小;用等式表示线段 , , 之间的数量关系,并证明;
(2)过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.

△ABC为等边三角形, , 于点D,E为线段 上一点, .以AE为边在直线 右侧构造等边三角形 ,连接 ,N为 的中点.
(1)如图1, 交于点G,连接 ,求线段 的长;
(2)如图2,将 绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接 , .当 时,猜想∠DNM的大小是否为定值,并证明你的结论;
(3)连接BN,在 绕点A逆时针旋转过程中,当线段BN最大时,请直接写出 的面积.

发现规律
(1)如图①, 与 都是等边三角形,直线 , 交于点 .直线 , 交于点 .求 的度数.
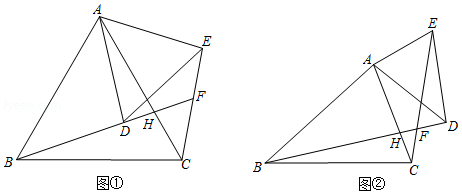
(2)已知: 与 的位置如图②所示,直线 , 交于点 .直线 , 交于点 .若 , ,求 的度数.
应用结论
(3)如图③,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 , 为 轴上一动点,连接 .将线段 绕点 逆时针旋转 得到线段 ,连接 , .求线段 长度的最小值.
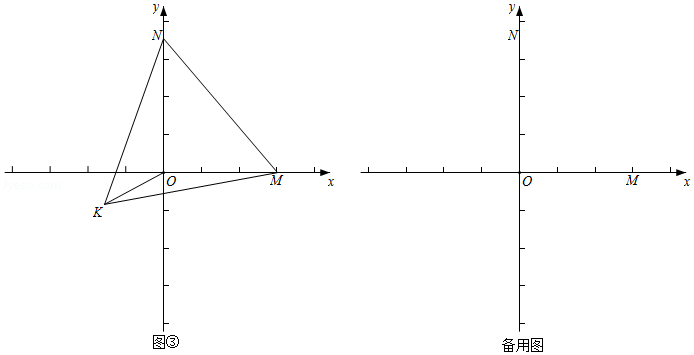
如图,在菱形 中, ,点 , , 分别在边 , 上, , 平分 ,点 是线段 上一动点(与点 不重合).
(1)求证: ;
(2)当 , 时.
求 周长的最小值;
②若点 是 的中点,是否存在直线 将 分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为 .若存在,请求出 的值;若不存在,请说明理由.
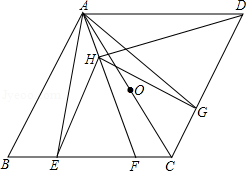
如图1,在等腰三角形 中, , ,点 、 分别在边 、 上, ,连接 ,点 、 、 分别为 、 、 的中点.
(1)观察猜想.
图1中,线段 、 的数量关系是 , 的大小为 .
(2)探究证明
把 绕点 顺时针方向旋转到如图2所示的位置,连接 、 、 ,判断 的形状,并说明理由;
(3)拓展延伸
把 绕点 在平面内自由旋转,若 , ,请求出 面积的最大值.
如图1,矩形 中, , , 中, , , , 的延长线相交于点 ,且 , , .将 绕点 逆时针旋转 得到△ .
(1)当 时,求点 到直线 的距离.
(2)在图1中,取 的中点 ,连结 ,如图2.
①当 与矩形 的一条边平行时,求点 到直线 的距离.
②当线段 与矩形 的边有且只有一个交点时,求该交点到直线 的距离的取值范围.

[性质探究]
如图,在矩形 中,对角线 , 相交于点 , 平分 ,交 于点 .作 于点 ,分别交 , 于点 , .
(1)判断 的形状并说明理由.
(2)求证: .
[迁移应用]
(3)记 的面积为 , 的面积为 ,当 时,求 的值.
[拓展延伸]
(4)若 交射线 于点 ,[性质探究]中的其余条件不变,连结 ,当 的面积为矩形 面积的 时,请直接写出 的值.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

如图1,已知四边形 是矩形,点 在 的延长线上, . 与 相交于点 ,与 相交于点 , .
(1)求证: ;
(2)若 ,求 的长;
(3)如图2,连接 ,求证: .

如图,在 中, , ,点 是 边上一动点,连接 ,把 绕点 逆时针旋转 ,得到 ,连接 , .点 是 的中点,连接 .
(1)求证: ;
(2)如图2所示,在点 运动的过程中,当 时,分别延长 , ,相交于点 ,猜想 与 存在的数量关系,并证明你猜想的结论;
(3)在点 运动的过程中,在线段 上存在一点 ,使 的值最小.当 的值取得最小值时, 的长为 ,请直接用含 的式子表示 的长.

已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
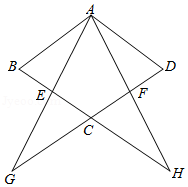
[小题1]求证: ;
[小题2]如果 ,求证: .
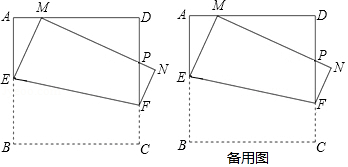
如图,在边长为1的正方形 中,动点 、 分别在边 、 上,将正方形 沿直线 折叠,使点 的对应点 始终落在边 上(点 不与点 、 重合),点 落在点 处, 与 交于点 ,设 .
(1)当 时,求 的值;
(2)随着点 在边 上位置的变化, 的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;
(3)设四边形 的面积为 ,求 与 之间的函数表达式,并求出 的最小值.
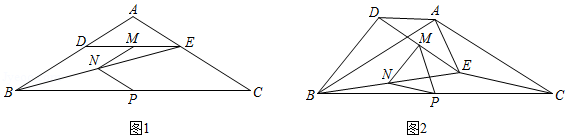
在数学兴趣小组活动中,小亮进行数学探究活动. 是边长为2的等边三角形, 是 上一点,小亮以 为边向 的右侧作等边三角形 ,连接 .
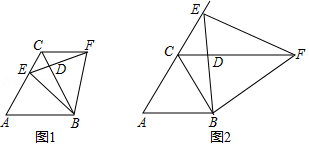
(1)如图1,当点 在线段 上时, 、 相交于点 ,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点 在线段 上运动时,点 也随着运动,若四边形 的面积为 ,求 的长.
(3)如图2,当点 在 的延长线上运动时, 、 相交于点 ,请你探求 的面积 与 的面积 之间的数量关系.并说明理由.
(4)如图2,当 的面积 时,求 的长.
已知, 中, , 是 边上一点,作 ,分别交边 , 于点 , .
(1)若 (如图 ,求证: .
(2)若 ,过点 作 ,交 (或 的延长线)于点 .试猜想:线段 , 和 之间的数量关系,并就 情形(如图 说明理由.
(3)若点 与 重合(如图 , ,且 .
①求 的度数;
②设 , , ,试证明: .

试题篮
()