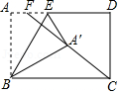
如图,矩形 中, , ,点 为 上一点,且 ,将 沿 翻折,得到△ ,连接 并延长,与 相交于点 ,则 的长为 .
在 中, , ,点 是 上一点,连接 ,过点 作 ,在 上取点 ,连接 .延长 至 ,使 ,连接 , ,且 .
(1)若 ,求 的长;
(2)如图1,当点 在 上时,求证: ;
(3)如图2,当点 在 的垂直平分线上时,直接写出 的值.

如图,在 中, 平分 交 于点 ,过点 作 交 于点 ,且 平分 ,若 ,则 的长为

A.4B.6C. D.8
如图, ,以点 为圆心,以任意长为半径作弧交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;以 为端点作射线 ,在射线 上截取线段 ,则 点到 的距离为

A.6B.2C.3D.
如图,已知 ,点 、 在射线 上(点 在点 、 之间),半径长为2的 与直线 相切,半径长为3的 与 相交,那么 的取值范围是

| A. |
|
B. |
|
C. |
|
D. |
|
四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形 的内角,正方形 变为菱形 .若 ,则菱形 的面积与正方形 的面积之比是

A.1B. C. D.
(年青海省中考)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.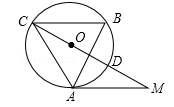
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
(年贵州省贵阳市)小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .
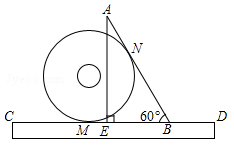
图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形 的对角线 上,时钟中心在矩形 对角线的交点 上.若 ,则 长为 (结果保留根号).
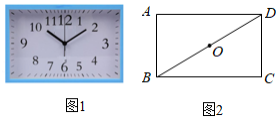
将一物体(视为边长为 米的正方形 从地面 上挪到货车车厢内.如图所示,刚开始点 与斜面 上的点 重合,先将该物体绕点 (E)按逆时针方向旋转至正方形 的位置,再将其沿 方向平移至正方形 的位置(此时点 与点 重合),最后将物体移到车厢平台面 上.已知 , ,过点 作 于点 , 米, 米.
(1)求线段 的长度;
(2)求在此过程中点 运动至点 所经过的路程.

试题篮
()