如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且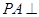 底面ABCD,
底面ABCD,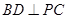 ,E是PA的中点.
,E是PA的中点.

(1)求证:平面 平面EBD;
平面EBD;
(2)若PA=AB=2,求三棱锥P-EBD的高.
如图在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
(1)证明:平面A1AC⊥平面AB1B;
(2)若点P为B1C1的中点,求三棱锥P-ABC与四棱锥P-AA1B1B的体积之比.
三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为()
A. |
B. |
C. |
D. |
如图,在三棱柱 中,
中, ,顶点
,顶点 在底面
在底面 上的射影恰为点
上的射影恰为点 ,
, .
.
(1)证明:平面 平面
平面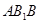 ;
;
(2 )若点 为
为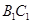 的中点,求出二面角
的中点,求出二面角 的余弦值.
的余弦值.
(1)证明:平面 平面
平面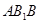 ;
;
(2)若点 为
为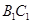 的中点,求出二面角
的中点,求出二面角 的余弦值.
的余弦值.
如图,在五面体 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求五面体 的体积.
的体积.
正四面体ABCD的棱长为1,其中线段AB 平面
平面 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面 上的射影
上的射影 长的范围是( )
长的范围是( )
A.[0, ] ] |
B.[ , , ] ] |
C.[ , , ] ] |
D.[ , , ] ] |
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
(1)求证:AC⊥B1C;
(2)若D是AB中点,求证:AC1∥平面B1CD.
已知三条不重合的直线m,n,l 和两个不重合的平面α,β ,下列命题正确的是:( )
A.若m//n,n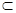 α,则m// α α,则m// α |
B.若α⊥β, α β="m," n⊥m ,则n⊥α. β="m," n⊥m ,则n⊥α. |
| C.若l⊥n ,m⊥n,则l//m |
| D.若l⊥α,m⊥β, 且l⊥m ,则α⊥β |
如图,等边三角形 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( ) 
A.动点 在平面 在平面 上的射影在线段 上的射影在线段 上 上 |
B.恒有平面 ⊥平面 ⊥平面 |
C.三棱锥 的体积有最大值 的体积有最大值 |
D.异面直线 与 与 不可能垂直 不可能垂直 |
在如图所示的几何体中,四边形 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ,
, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求四面体 的体积;
的体积;
(3)线段 上是否存在点
上是否存在点 ,使
,使 平面
平面 ?请证明你的结论.
?请证明你的结论.
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.
(1)求证:BC1∥平面CA1D;
(2)求证:平面CA1D⊥平面AA1B1B;
(3)若底面ABC为边长为2的正三角形,BB1= 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.
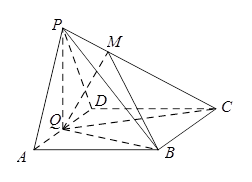
如图在四棱锥 中,底面
中,底面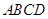 是菱形,
是菱形,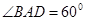 ,平面
,平面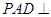 平面
平面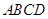 ,
, ,
,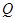 为
为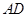 的中点,
的中点,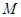 是棱
是棱 上一点,且
上一点,且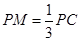 .
.
(1)求证: 平面
平面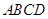 ;
;
(2)证明: ∥平面
∥平面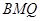 ;
;
(3)求二面角 的度数.
的度数.
试题篮
()