设 ,
, ,
, 是空间三条直线,
是空间三条直线, ,
, 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )
A.当 时,若 时,若 ,则 ,则 |
B.当 时,若 时,若 ,则 ,则 |
C.当 ,且 ,且 是 是 在 在 内的射影时,若 内的射影时,若 ,则 ,则 |
D.当 ,且 ,且 时,若 时,若 ,则 ,则 |
l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )
| A.l1⊥l2,l2⊥l3⇒l1∥l3 |
| B.l1⊥l2,l2∥l3⇒l1⊥l3 |
| C.l1∥l2∥l3⇒l1,l2,l3共面 |
| D.l1,l2,l3共点⇒l1,l2,l3共面 |
设 是两个不同的平面,
是两个不同的平面,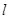 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则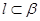 |
B.若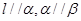 ,则 ,则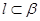 |
C.若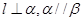 ,则 ,则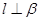 |
D.若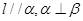 ,则 ,则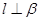 |
设 是两条不同的直线,
是两条不同的直线,  是两个不同的平面,下列命题中错误的是( )
是两个不同的平面,下列命题中错误的是( )
A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( ).
| A.α∥β且l∥α |
| B.α⊥β且l⊥β |
| C.α与β相交,且交线垂直于l |
| D.α与β相交,且交线平行于l |
已知 是两条不重合的直线,
是两条不重合的直线, ,
, ,
, 是三个两两不重合的平面,给出下列四
是三个两两不重合的平面,给出下列四
个命题:
①若 则
则 ;
;
②若 则
则 ;
;
③若 则
则 ;
;
④若 是异面直线,
是异面直线, 则
则 .
.
其中正确命题的序号是 ( )
| A.①和④ | B.①和③ | C.③和④ | D.①和② |
给定下列两个关于异面直线的命题:那么( )
命题(1):若平面 上的直线
上的直线 与平面
与平面 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是 与
与 的交线,那么
的交线,那么 至多与
至多与 中的一条相交;
中的一条相交;
命题(2):不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
| A.命题(1)正确,命题(2)不正确 |
| B.命题(2)正确,命题(1)不正确 |
| C.两个命题都正确 |
| D.两个命题都不正确 |
如图所示,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠A=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )

| A.直线AC上 | B.直线AB上 |
| C.直线BC上 | D.△ABC内部 |
试题篮
()