(12分) 若二次函数f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
且f(-2)>f(3),设m>-n>0.
(1) 试证明函数f(x)在(0,+∞)上是减函数;
(2) 试比较f(m)和f(n)的大小,并说明理由.
函数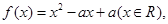 数列
数列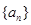 的前
的前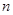 项和
项和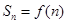 ,且
,且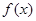 同时满足:①不等式
同时满足:①不等式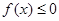 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在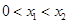 ,使得不等式
,使得不等式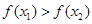 成立.
成立.
(1)求函数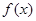 的表达式;
的表达式;
(2)求数列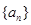 的通项公式.
的通项公式.
(本小题满分12分)
设平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求:
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)求圆 的方程;
的方程;
(Ⅲ)问圆 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
已知二次函数f(x)=ax2+bx+c (a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,f(x)≤ .
.
(1)求f(1)的值;
(2)证明:a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx (x∈R)是单调函数,求证:m≤0或m≥1.
已知当x=5时,二次函数f(x)=ax2+bx取得最小值,等差数列{an}的前n项和Sn=f(n),a2=-7.
(1)求数列{an}的通项公式;
(2)数列{bn}的前n项和为Tn,且bn= ,求Tn.
,求Tn.
已知函数
(1)若函数在 的单调递减区间(—∞,2],求函数
的单调递减区间(—∞,2],求函数 在区间[3,5]上的最大值.
在区间[3,5]上的最大值.
(2)若函数在 在单区间(—∞,2]上是单调递减,求函数
在单区间(—∞,2]上是单调递减,求函数 的最大值.
的最大值.
试题篮
()