用数学归纳法证明某命题时,左式为 (n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.
(n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.
某个命题与正整数n有关,如果当 时命题成立,那么可推得当
时命题成立,那么可推得当 时命题也成立. 现已知当
时命题也成立. 现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
| A.当n=6时该命题不成立 | B.当n=6时该命题成立 |
| C.当n=8时该命题不成立 | D.当n=8时该命题成立 |
利用数学归纳法证明“1+a+a2+…+an+1 = , (a≠1,n∈N)”时,在验证n=1成立时,左边应该是 ( )
, (a≠1,n∈N)”时,在验证n=1成立时,左边应该是 ( )
| A.1 | B.1+a | C.1+a+a2 | D.1+a+a2+a3 |
如果命题P(n)对n=k成立,则它对n=k+1也成立,现已知P(n)对n=4不成立,则下列结论正确的是( )
| A.P(n)对n∈N*成立 | B.P(n)对n>4且n∈N*成立 |
| C.P(n)对n<4且n∈N*成立 | D.P(n)对n≤4且n∈N*不成立 |
用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”,从“k到k+1”左端需增乘的代数式为( )
| A.2k+1 | B.2(2k+1) | C. |
D. |
设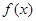 是定义在正整数集上的函数且满足当
是定义在正整数集上的函数且满足当 成立时,总可以推出
成立时,总可以推出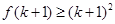 成立,则下列命题总成立的是( )
成立,则下列命题总成立的是( )
A.若 成立 成立 |
B.若 成立,则 成立,则 成立 成立 |
C.若 成立,则当 成立,则当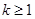 时,均有 时,均有 成立 成立 |
D.若 成立,则当 成立,则当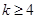 时,均有 时,均有 成立 成立 |
已知经过计算和验证有下列正确的不等式: ,
, ,
, ,
, ,
, ,根据以上不等式的规律,写出一个一般性的不等式 .
,根据以上不等式的规律,写出一个一般性的不等式 .
用数学归纳法证明 时,假设n=k时命题成立,则当n=k+1时,左端增加的项数是 ( )
时,假设n=k时命题成立,则当n=k+1时,左端增加的项数是 ( )
| A.1项 | B. 项 项 |
C. 项 项 |
D. 项 项 |
利用数学归纳法证明不等式1+ +
+ +…+
+…+ < f(n) (n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
< f(n) (n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C. 项 项 |
D. 项 项 |
试题篮
()