高中数学三面角、直三面角的基本性质解答题

（本小题满分12分）已知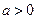,设命题函数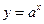在R上单调递减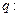，不等式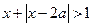的解集为R,若和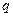中有且只有一个命题为真命题，求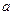的取值范围.

养路处建造无底的圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用），已建的仓库的底面直径为12米，高4米。养路处拟另建一个更大的圆锥形仓库，以存放更多食盐。现有两种方案：一是新建的仓库的底面直径比原来增加4米（高不变）；二是高度增加4米(底面直径不变)。
分别计算按这两种方案所建的仓库的体积；
分别计算按这两种方案所建的仓库的表面积；
哪个方案更经济些？

为了提高产品的年产量，某企业拟在2010年进行技术改革．经调查测算，产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x＝3－(k为常数)．如果不搞技术改革，则该产品当年的产量只能是1万件．已知2010年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元．由于市场行情较好，厂家生产的产品均能销售出去．厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)．
(1)将2010年该产品的利润y万元(利润＝销售金额－生产成本－技术改革费用)表示为技术改革费用m万元的函数；
(2)该企业2010年的技术改革费用投入多少万元时，厂家的利润最大？

定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界.
（1）判断函数是否是有界函数，请写出详细判断过程；
（2）试证明：设，若在上分别以为上界，
求证：函数在上以为上界；
（3）若函数在上是以3为上界的有界函数，
求实数的取值范围.

（本小题满分13分）
为了预防甲型流感，某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，y与t的函数关系式为（a为常数），如图所示，根据图中提供的信息，回答下列问题：
（1）求从药物释放开始，每立方米空气中的含药量y（毫克）与时间t（小时）之间的函数关系式；
（2）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那从药物释放开始，至少需要经过多少小时后，学生才能回到教室．

设不等式 $\left|x-2\right|<a(a\in N^{{*}^{}})$的解集为A,且 $\frac{3}{2}\in A,\frac{1}{2}\notin A$.

（Ⅰ）求 $a$的值

（Ⅱ）求函数 $f\left(x\right)=\left|x+a\right|+\left|x-2\right|$的最小值

要在墙上开一个上部为半圆，下部为矩形的窗户
（如图所示），在窗框总长度为的条件下，

（1）请写出窗户的面积与圆的直径的函数关系；
（2）要使窗户透光面积最大，窗户应具有怎样的尺寸？并写出最大值.

已知函数满足0＜＜1。
（1）求的取值范围；
（2）若是偶函数且满足，当时，有，求 在上的解析式。

已知函数
⑴解不等式；
⑵若不等式的解集为空集，求的取值范围.

设函数是定义域为的奇函数．
(Ⅰ)求的值；
(Ⅱ)若，且在上的最小值为，求的值.

已知函数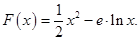
（I）求函数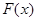的极值；
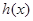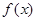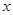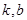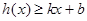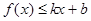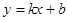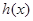（II）对于函数和定义域内的任意实数,若存在常数,使得不等式和都成立,则称直线是函数和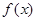的“分界线”．
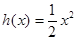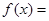
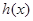设函数，，试问函数和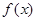是否存在“分界线”？若存在，求出“分界线”的方程．若不存在请说明理由．

设 
（1）当，求的取值范围；
（2）若对任意，恒成立，求实数的最小值．

已知某公司生产某品牌服装的年固定成本为10万元，每生产千件需另投入2.7万元，设该公司年内共生产该品牌服装千件并全部销售完，每千件的销售收入为万元，且．
(1）写出年利润（万元）关于年产品（千件）的函数解析式；
(2）年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？
(注：年利润=年销售收入－年总成本）

已知函数的定义域是，且满足，，如果对于0<x<y，都有，
（1）求；
（2）解不等式

(本题满分16分)
已知函数，其中，
（1）当时，把函数写成分段函数的形式；
（2）当时，求在区间上的最值；
（3）设，函数在上既有最大值又有最小值，请分别求出的取值范围（用表示）．