(本小题满分12分)如图,在斜三棱柱 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
(本小题满分14分)如图,四棱锥P—ABCD的底面是边长为1的正方形,PD^底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF^PB.
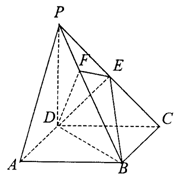
(1)证明:PA//平面EDB;
(2)证明:AC^DF;
(3)求三棱锥B—ADF的体积.
(本小题12分)第(1)小题5分,第(2)题7分
如图,在四棱锥中 中,底面
中,底面 为菱形,
为菱形, ,
, ,点
,点 在线段
在线段 上,且
上,且 ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若平面 平面
平面 ,求三棱锥
,求三棱锥 的体积;
的体积;
(本小题满分12分)斜三棱柱 中,侧面
中,侧面
 底面ABC,侧面
底面ABC,侧面 是菱形,
是菱形, ,
, ,
, ,E、F分别是
,E、F分别是 ,AB的中点.
,AB的中点.
(1)求证:EF∥平面 ;
;
(2)求证:CE⊥面ABC.
(3)求四棱锥 的体积.
的体积.
本题共有2小题,第(1)小题满分6分,第(2)小题满分8分.
如图,在长方体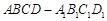 中,
中,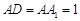 ,
,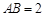 ,点
,点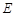 在棱
在棱 上移动.
上移动.
(1)当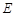 为
为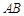 的中点时,求四面体
的中点时,求四面体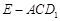 的体积;
的体积;
(2)证明: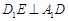 .
.
如图,已知圆锥的底面半径为 ,点Q为半圆弧
,点Q为半圆弧 的中点,点
的中点,点 为母线
为母线 的中点.若直线
的中点.若直线 与
与 所成的角为
所成的角为 ,求此圆锥的表面积.
,求此圆锥的表面积.
(本题满分12分,第(Ⅰ)问6分,第(Ⅱ)问6分)如图一, 是正三角形,
是正三角形, 是等腰直角三角形,
是等腰直角三角形, .将
.将 沿
沿 折起,使得
折起,使得 , 如图二,
, 如图二, 为
为 的中点
的中点
(Ⅰ)求证: ;
;
(Ⅱ)求 的面积;
的面积;
(Ⅲ)求三棱锥 的体积.
的体积.
)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为 ,求
,求 .
.
(本小题满分14分)如图,已知三棱锥A—BPC中,AP⊥PC, AC⊥BC,M为AB中点,D为PB中点, 且△PMB为正三角形.
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D—BCM的体积.
(本小题满分15分)如图所示,正方形 与直角梯形
与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求四面体 的体积.
的体积.
如图,在矩形 中,点
中,点 为边
为边 上的点,点
上的点,点 为边
为边 的中点,
的中点,  ,现将
,现将 沿
沿 边折至
边折至 位置,且平面
位置,且平面 平面
平面 .
.


(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求四棱锥 的体积.
的体积.
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面 均为边长为1的等边三角形,
均为边长为1的等边三角形, ,
, 为
为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)证明: ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
【原创】如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, , 若
, 若
 ,
,
且侧面 底面
底面 .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)侧棱 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求三棱锥 的体积.
的体积.
【改编】如图,在边长为1的等边三角形 中,
中, 分别是
分别是 边上的点,
边上的点, ,
, 是
是 的中点,
的中点, 与
与 交于点
交于点 ,将
,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,得到如图所示的三棱锥
,得到如图所示的三棱锥 .
.
(1)证明: //平面
//平面 ;
;
(2)证明:
 平面
平面 ;
;
(3)当 时,求三棱锥
时,求三棱锥 的体积
的体积 .
.
试题篮
()