初中数学解直角三角形的应用解答题

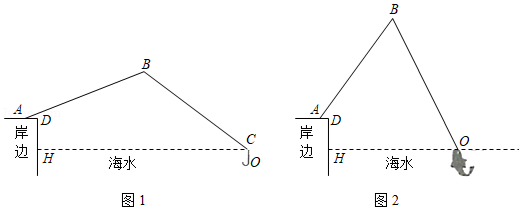
我市的前三岛是众多海钓人的梦想之地．小明的爸爸周末去前三岛钓鱼，将鱼竿 $\mathit{AB}$ 摆成如图1所示．已知 $\mathit{AB}=4.8m$ ，鱼竿尾端 $A$ 离岸边 $0.4m$ ，即 $\mathit{AD}=0.4m$ ．海面与地面 $\mathit{AD}$ 平行且相距 $1.2m$ ，即 $\mathit{DH}=1.2m$ ．

（1）如图1，在无鱼上钩时，海面上方的鱼线 $\mathit{BC}$ 与海面 $\mathit{HC}$ 的夹角 $\angle \mathit{BCH}=37°$ ，海面下方的鱼线 $\mathit{CO}$ 与海面 $\mathit{HC}$ 垂直，鱼竿 $\mathit{AB}$ 与地面 $\mathit{AD}$ 的夹角 $\angle \mathit{BAD}=22°$ ．求点 $O$ 到岸边 $\mathit{DH}$ 的距离；

（2）如图2，在有鱼上钩时，鱼竿与地面的夹角 $\angle \mathit{BAD}=53°$ ，此时鱼线被拉直，鱼线 $\mathit{BO}=5.46m$ ，点 $O$ 恰好位于海面．求点 $O$ 到岸边 $\mathit{DH}$ 的距离．

（参考数据： $\sin 37°=\cos 53°\approx \frac{3}{5}$ ， $\cos 37°=\sin 53°\approx \frac{4}{5}$ ， $\tan 37°\approx \frac{3}{4}$ ， $\sin 22°\approx \frac{3}{8}$ ， $\cos 22°\approx \frac{15}{16}$ ， $\tan 22°\approx \frac{2}{5})$

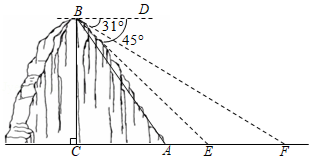
某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥．如图，该河旁有一座小山，山高 $\mathit{BC}=80m$ ，坡面 $\mathit{AB}$ 的坡度 $i=1:0.7$ （注：坡度 $i$ 是指坡面的铅直高度与水平宽度的比），点 $C$ 、 $A$ 与河岸 $E$ 、 $F$ 在同一水平线上，从山顶 $B$ 处测得河岸 $E$ 和对岸 $F$ 的俯角分别为 $\angle \mathit{DBE}=45°$ ， $\angle \mathit{DBF}=31°$ ．

（1）求山脚 $A$ 到河岸 $E$ 的距离；

（2）若在此处建桥，试求河宽 $\mathit{EF}$ 的长度．（结果精确到 $0.1m)$

（参考数据： $\sin 31°\approx 0.52$ ， $\cos 31°\approx 0.86$ ， $\tan 31°\approx 0.60)$

已知锐角 $\mathit{\Delta ABC}$ 中，角 $A$ 、 $B$ 、 $C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ，边角总满足关系式： $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$ ．

（1）如图1，若 $a=6$ ， $\angle B=45°$ ， $\angle C=75°$ ，求 $b$ 的值；

（2）某公园准备在园内一个锐角三角形水池 $\mathit{ABC}$ 中建一座小型景观桥 $\mathit{CD}$ （如图2所示），若 $\mathit{CD}\perp \mathit{AB}$ ， $\mathit{AC}=14$ 米， $\mathit{AB}=10$ 米， $\sin \angle \mathit{ACB}=\frac{5\sqrt{3}}{14}$ ，求景观桥 $\mathit{CD}$ 的长度．

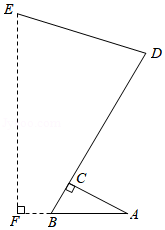
一种可折叠的医疗器械放置在水平地面上，这种医疗器械的侧面结构如图实线所示，底座为 $\mathit{\Delta ABC}$，点 $B$、 $C$、 $D$在同一条直线上，测得 $\angle \mathit{ACB}=90°$， $\angle \mathit{ABC}=60°$， $\mathit{AB}=32\mathit{cm}$， $\angle \mathit{BDE}=75°$，其中一段支撑杆 $\mathit{CD}=84\mathit{cm}$，另一段支撑杆 $\mathit{DE}=70\mathit{cm}$．求支撑杆上的点 $E$到水平地面的距离 $\mathit{EF}$是多少？（用四舍五入法对结果取整数，参考数据： $\sin 15°\approx 0.26$， $\cos 15°\approx 0.97$， $\tan 15°\approx 0.27$， $\sqrt{3}\approx 1.732)$

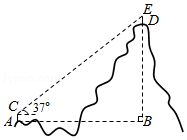
如图1是平凉市地标建筑“大明宝塔”，始建于明嘉靖十四年 $(1535$年），是明代平凉韩王府延恩寺的主体建筑．宝塔建造工艺精湛，与崆峒山的凌空塔遥相呼应，被誉为平凉古塔“双璧”．某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动，具体过程如下：

方案设计：如图2，宝塔 $\mathit{CD}$垂直于地面，在地面上选取 $A$， $B$两处分别测得 $\angle \mathit{CAD}$和 $\angle \mathit{CBD}$的度数 $(A$， $D$， $B$在同一条直线上）．

数据收集：通过实地测量：地面上 $A$， $B$两点的距离为 $58m$， $\angle \mathit{CAD}=42°$， $\angle \mathit{CBD}=58°$．

问题解决：求宝塔 $\mathit{CD}$的高度（结果保留一位小数）．

参考数据： $\sin 42°\approx 0.67$， $\cos 42°\approx 0.74$， $\tan 42°\approx 0.90$， $\sin 58°\approx 0.85$， $\cos 58°\approx 0.53$， $\tan 58°\approx 1.60$．

根据上述方案及数据，请你完成求解过程．

为进一步加强疫情防控工作，避免在测温过程中出现人员聚集现象，某学校决定安装，该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，无需人员停留和接触，安装说明书的部分内容如表．

名称	红外线体温检测仪
安装示意图
技术参数	探测最大角： $\angle \mathit{OBC}＝73.14°$
	探测最小角： $\angle \mathit{OAC}＝30.97°$
安装要求	本设备需安装在垂直于水平地面AC的支架CP上

根据以上内容，解决问题：

学校要求测温区域的宽度AB为4m，请你帮助学校确定该设备的安装高度OC．

（结果精确到0.1m，参考数据： $\mathit{sin}73.14°\approx 0.957，\mathit{cos}73.14°\approx 0.290$，t $\mathit{an}73.14°\approx 3.300$， $\mathit{sin}30.97°\approx 0.515$， $\mathit{cos}30.97°\approx 0.857$， $\text{t}\mathit{an}30.97°\approx 0.600$）

如图，著名旅游景区 $B$位于大山深处，原来到此旅游需要绕行 $C$地，沿折线 $A\to C\to B$方可到达．当地政府为了增强景区的吸引力，发展壮大旅游经济，修建了一条从 $A$地到景区 $B$的笔直公路．请结合 $\angle A=45°$， $\angle B=30°$， $\mathit{BC}=100$千米， $\sqrt{2}\approx 1.4$， $\sqrt{3}\approx 1.7$等数据信息，解答下列问题：

（1）公路修建后，从 $A$地到景区 $B$旅游可以少走多少千米？

（2）为迎接旅游旺季的到来，修建公路时，施工队使用了新的施工技术，实际工作时每天的工效比原计划增加 $25\%$，结果提前50天完成了施工任务．求施工队原计划每天修建多少千米？

今年疫情期间，针对各种入口处人工测量体温存在的感染风险高、效率低等问题，清华大学牵头研制一款“测温机器人”，如图1，机器人工作时，行人抬手在测温头处测量手腕温度，体温合格则机器人抬起臂杆行人可通行，不合格时机器人不抬臂杆并报警，从而有效阻隔病原体．

（1）为了设计“测温机器人”的高度，科研团队采集了大量数据．下表是抽样采集某一地区居民的身高数据：

测量对象	男性 $(18~60$岁）				女性 $(18~55$岁）
抽样人数（人 $)$	2000	5000	20000	2000		5000	20000
平均身高（厘米）	173	175	176	164		165	164

根据你所学的知识，若要更准确的表示这一地区男、女的平均身高，男性应采用　176　厘米，女性应采用　　厘米；

（2）如图2，一般的，人抬手的高度与身高之比为黄金比时给人的感觉最舒适，由此利用（1）中的数据得出测温头点 $P$距地面105厘米．指示牌挂在两臂杆 $\mathit{AB}$， $\mathit{AC}$的连接点 $A$处， $A$点距地面110厘米．臂杆落下时两端点 $B$， $C$在同一水平线上， $\mathit{BC}=100$厘米，点 $C$在点 $P$的正下方5厘米处．若两臂杆长度相等，求两臂杆的夹角．

（参考数据表）

计算器按键顺序	计算结果（近似值）	计算器按键顺序	计算结果（近似值）
	0.1		78.7
	0.2		84.3
	1.7		5.7
	3.5		11.3

人字折叠梯完全打开后如图1所示， $B$， $C$是折叠梯的两个着地点， $D$是折叠梯最高级踏板的固定点．图2是它的示意图， $\mathit{AB}=\mathit{AC}$， $\mathit{BD}=140\mathit{cm}$， $\angle \mathit{BAC}=40°$，求点 $D$离地面的高度 $\mathit{DE}$．（结果精确到 $0.1\mathit{cm}$；参考数据 $\sin 70°\approx 0.94$， $\cos 70°\approx 0.34$， $\sin 20°\approx 0.34$， $\cos 20°\approx 0.94)$

如图1为搭建在地面上的遮阳棚，图2、图3是遮阳棚支架的示意图．遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块 $E$， $H$可分别沿等长的立柱 $\mathit{AB}$， $\mathit{DC}$上下移动， $\mathit{AF}=\mathit{EF}=\mathit{FG}=1m$．

（1）若移动滑块使 $\mathit{AE}=\mathit{EF}$，求 $\angle \mathit{AFE}$的度数和棚宽 $\mathit{BC}$的长．

（2）当 $\angle \mathit{AFE}$由 $60°$变为 $74°$时，问棚宽 $\mathit{BC}$是增加还是减少？增加或减少了多少？

（结果精确到 $0.1m$，参考数据： $\sqrt{3}\approx 1.73$， $\sin 37°\approx 0.60$， $\cos 37°\approx 0.80$， $\tan 37°\approx 0.75)$

图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成．当位于顶端的小挂锁打开时，钢条可放入底盒中（底盒固定在地面下），此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位．图2是其示意图，经测量，钢条 $\mathit{AB}=\mathit{AC}=50\mathit{cm}$， $\angle \mathit{ABC}=47°$．

（1）求车位锁的底盒长 $\mathit{BC}$．

（2）若一辆汽车的底盘高度为 $30\mathit{cm}$，当车位锁上锁时，问这辆汽车能否进入该车位？

（参考数据： $\sin 47°\approx 0.73$， $\cos 47°\approx 0.68$， $\tan 47°\approx 1.07)$

有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度．图2是这种升降熨烫台的平面示意图． $\mathit{AB}$和 $\mathit{CD}$是两根相同长度的活动支撑杆，点 $O$是它们的连接点， $\mathit{OA}=\mathit{OC}$， $h\left(\mathit{cm}\right)$表示熨烫台的高度．

（1）如图 $2-1$．若 $\mathit{AB}=\mathit{CD}=110\mathit{cm}$， $\angle \mathit{AOC}=120°$，求 $h$的值；

（2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为 $120\mathit{cm}$时，两根支撑杆的夹角 $\angle \mathit{AOC}$是 $74°$（如图 $2-2)$．求该熨烫台支撑杆 $\mathit{AB}$的长度（结果精确到 $1\mathit{cm})$．

（参考数据： $\sin 37°\approx 0.6$， $\cos 37°\approx 0.8$， $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6)$

如图， $A$， $B$两点被池塘隔开，在 $\mathit{AB}$外选一点 $C$，连接 $\mathit{AC}$， $\mathit{BC}$．测得 $\mathit{BC}=221m$， $\angle \mathit{ACB}=45°$， $\angle \mathit{ABC}=58°$．根据测得的数据，求 $\mathit{AB}$的长（结果取整数）．

参考数据： $\sin 58°\approx 0.85$， $\cos 58°\approx 0.53$， $\tan 58°\approx 1.60$．

[材料阅读]2020年5月27日，2020珠峰高程测量登山队成功登顶珠穆朗玛峰，将用中国科技“定义”世界新高度．其基本原理之一是三角高程测量法，在山顶上立一个觇标，找到2个以上测量点，分段测量山的高度，再进行累加．因为地球面并不是水平的，光线在空气中会发生折射，所以当两个测量点的水平距离大于 $300m$时，还要考虑球气差，球气差计算公式为 $f=\frac{0.43d^2}{R}$（其中 $d$为两点间的水平距离， $R$为地球的半径， $R$取 $6400000m)$，即：山的海拔高度 $=$测量点测得山的高度 $+$测量点的海拔高度 $+$球气差．

[问题解决]某校科技小组的同学参加了一项野外测量某座山的海拔高度活动．如图，点 $A$， $B$的水平距离 $d=800m$，测量仪 $\mathit{AC}=1.5m$，觇标 $\mathit{DE}=2m$，点 $E$， $D$， $B$在垂直于地面的一条直线上，在测量点 $A$处用测量仪测得山顶觇标顶端 $E$的仰角为 $37°$，测量点 $A$处的海拔高度为 $1800m$．

（1）数据6400000用科学记数法表示为　 $6.4\times {10}^6$　；

（2）请你计算该山的海拔高度．（要计算球气差，结果精确到 $0.01m)$

（参考数据： $\sin 37°\approx 0.60$， $\cos 37°\approx 0.80$， $\tan 37°\approx 0.75)$

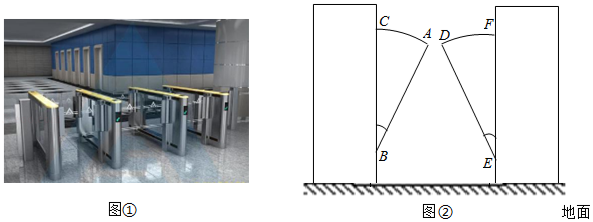
图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形 $\mathit{ABC}$和 $\mathit{DEF}$是闸机的“圆弧翼”，两圆弧翼成轴对称， $\mathit{BC}$和 $\mathit{EF}$均垂直于地面，扇形的圆心角 $\angle \mathit{ABC}=\angle \mathit{DEF}=28°$，半径 $\mathit{BA}=\mathit{ED}=60\mathit{cm}$，点 $A$与点 $D$在同一水平线上，且它们之间的距离为 $10\mathit{cm}$．

（1）求闸机通道的宽度，即 $\mathit{BC}$与 $\mathit{EF}$之间的距离（参考数据： $\sin 28°\approx 0.47$， $\cos 28°\approx 0.88$， $\tan 28°\approx 0.53)$；

（2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的2倍，180人的团队通过一个智能闸机口比通过一个人工检票口可节约3分钟，求一个智能闸机平均每分钟检票通过的人数．