下面几个推理过程是演绎推理的是( )
| A.某同学第一次数学考试65分,第二次考试68分,由此预测其第三次考试71分. |
B.根据圆的面积为 ,推测球的体积为 ,推测球的体积为 . . |
C.在数列 中,根据 中,根据 ,计算出 ,计算出 的值,然后猜想 的值,然后猜想 的通项公式. 的通项公式. |
| D.因为平行四边形的对角线互相平分,而菱形是平行四边形,所以菱形的对角线互相平分 |
已知x∈R+,有不等式:x+ ≥2
≥2 =2,x+
=2,x+ =
= +
+ +
+ ≥3
≥3 =3,….启发我们可能推广结论为:x+
=3,….启发我们可能推广结论为:x+ ≥n+1(n∈N*),则a的值为 ( )
≥n+1(n∈N*),则a的值为 ( )
| A.2n | B.nn | C.n2 | D.2n+1 |
平面几何中,有边长为 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值 ,类比上述命题,棱长为
,类比上述命题,棱长为 的正四面体内任一点到四个面的距离之和为 ( )
的正四面体内任一点到四个面的距离之和为 ( )
A. |
B. |
C. |
D. |
设△ 的三边长分别为
的三边长分别为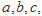 △
△ 的面积为
的面积为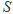 ,内切圆半径为
,内切圆半径为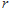 ,则
,则 .类比这个结论可知:四面体
.类比这个结论可知:四面体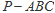 的四个面的面积分别为
的四个面的面积分别为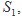
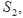

 内切球的半径为
内切球的半径为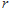 ,四面体
,四面体 的体积为
的体积为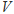 ,则
,则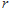 =( )
=( )
A.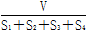 |
B.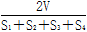 |
C.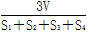 |
D.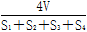 |
如下图所示将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>l,n∈N*)个点,相应
的图案中总的点数记为 ,则
,则 =( )
=( )

A. |
B. |
C. |
D. |
下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则 + + = = |
| B.由平面三角形的性质,推测空间四面体的性质 |
| C.某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人 |
D.在数列 中, 中, , , ,计算 ,计算 ,由此推测通项 ,由此推测通项 |
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, ,
, ,则第7行第4个数(从左往右数)为( )
,则第7行第4个数(从左往右数)为( )

A. |
B. |
C. |
D. |
“指数函数 是增函数,
是增函数, 是指数函数,所以
是指数函数,所以
 是增函数”,在以上演绎推理中,下列说法正确的是( )
是增函数”,在以上演绎推理中,下列说法正确的是( )
| A.推理完全正确 | B.大前提不正确 |
| C.小前提不正确 | D.推理形式不正确 |
法国数学家费马观察到 ,
, ,
, ,
, 都是质数,于是他提出猜想:任何形如
都是质数,于是他提出猜想:任何形如 N*)的数都是质数,这就是著名的费马猜想.半个世纪之后,善于发现的欧拉发现第5个费马数
N*)的数都是质数,这就是著名的费马猜想.半个世纪之后,善于发现的欧拉发现第5个费马数 不是质数,从而推翻了费马猜想,这一案例说明( )
不是质数,从而推翻了费马猜想,这一案例说明( )
| A.归纳推理,结果一定不正确 | B.归纳推理,结果不一定正确 |
| C.类比推理,结果一定不正确 | D.类比推理,结果不一定正确 |
试题篮
()