如图,四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
, ,
, ,
, ,
, ,
, 是
是 的中点,
的中点, 上的点
上的点 满足
满足 .
.
(Ⅰ)求证:
 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
已知平行四边形ABCD(图1)中,AB=4,BC=5,对角线AC=3,将三角形 ACD沿AC折起至
ACD沿AC折起至 PAC位置(图2),使二面角
PAC位置(图2),使二面角 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.

(1)求证:PC 平面BGH;
平面BGH;
(2)求平面PAB与平面BGH夹角的余弦值.
等边三角形 的边长为3,点
的边长为3,点 、
、 分别是边
分别是边 、
、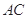 上的点,且满足
上的点,且满足
 (如图1).将△
(如图1).将△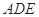 沿
沿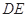 折起到△
折起到△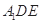 的位置,使二面角
的位置,使二面角 为直二面角,连结
为直二面角,连结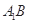 、
、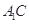 (如图2).
(如图2).
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)在线段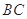 上是否存在点
上是否存在点 ,使直线
,使直线 与平面
与平面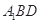 所成的角为
所成的角为 ?若存在,求出
?若存在,求出 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD//FE,∠AFE=60º,且平面ABCD⊥平面ADEF,AF=FE=AB= =2,点G为AC的中点.
=2,点G为AC的中点.
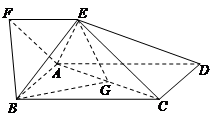
(Ⅰ)求证:EG//平面ABF;
(Ⅱ)求三棱锥B-AEG的体积;
(Ⅲ)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由.
如图,在三棱锥 底面ABC,且SB=
底面ABC,且SB= 分别是SA、SC的中点.
分别是SA、SC的中点.
(Ⅰ)求证:平面 平面BCD;
平面BCD;
(Ⅱ)求二面角 的平面角的大小.
的平面角的大小.
如图, 平面
平面 ,
, 是矩形,
是矩形, ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上的动点.
上的动点.
(Ⅰ)求三棱锥 的体积;
的体积;
(Ⅱ)当点 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅲ)证明:无论点 在边
在边 的何处,都有
的何处,都有 .
.
如图,已知 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求三棱锥 的体积;
的体积;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)若点 为线段
为线段 中点,求证:
中点,求证: ∥平面
∥平面 .
.
(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。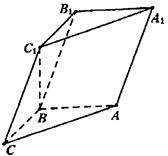
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设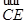 =λ
=λ (0≤A≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤A≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E、G分别是BC、PE的中点.
(1)求证:AD⊥PE;
(2)求二面角E-AD-G的正切值.
如图:长方形 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)试问:在线段 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 平面
平面 ?若存在,试指出点
?若存在,试指出点
的位置,并证明你的结论;若不存在,请说明理由.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:
(1)PA∥平面MDB;
(2)PD⊥BC.
试题篮
()