高中数学二次剩余试题

（．(本题满分12分)
已知二次函数和“伪二次函数” （、、），
（I）证明：只要，无论取何值，函数在定义域内不可能总为增函数；
（II）在二次函数图象上任意取不同两点，线段中点的横坐标为，记直线的斜率为，
（i）求证：；
（ii）对于“伪二次函数”，是否有（i）同样的性质?证明你的结论.

生产某种商品x件，所需费用为元，而售出x件这种商品时，每件的价格为p元，这里 (a，b是常数)。
（1）写出出售这种商品所获得的利润y元与售出这种商品的件数x间的函数关系式；
（2）如果生产出来的这种商品都能卖完，那么当产品是150件时，所获得的利润最大，并且这时的价格是40元，求a，b的值。

设，，函数。若对都成立，求的取值范围。

．(本题满分18分)
本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.
设二次函数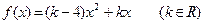，对任意实数，有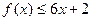恒成立；数列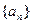满足.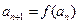
（1）求函数的解析式和值域；
（2）试写出一个区间，使得当时，数列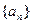在这个区间上是递增数列，
并说明理由；
（3）已知，是否存在非零整数，使得对任意，都有
 恒成立，若存在，
求之；若不存在，说明理由.

若函数，恒有，则a的最大值为（ ）

A．2

B．4

C．8

D．16

(本题满分16分)
已知函数
（Ⅰ）若函数是定义域上的单调函数，求实数的最小值；
（Ⅱ）在函数的图象上是否存在不同两点，线段的中点的横坐标为，直线的斜率为，有成立？若存在，请求出的值；若不存在，请说明理由．

（本小题满分12分）
已知函数和．其中．
（1）若函数与的图像的一个公共点恰好在x轴上，求的值；w
（2）若函数与图像相交于不同的两点A、B，O为坐标原点，试问：△OAB的面积S有没有最值？如果有，求出最值及所对应的的值；如果没有，请说明理由．
（3）若和是方程的两根，且满足，
证明：当时，．

设f(x)是定义在R上的偶函数，对x∈R，都有，且当时，，若在区间内关于x的方程恰有3个不同的实数根，则实数的取值范围是                       (    )

A．(1,2)

B．(2，＋∞)

C．(1)

D．（2)

函数在上为增函数，则的取值范围是          。

函数的图象在点处的切线与轴交点的横坐标为，            ，数列的通项公式为        ．

已知对任意实数x，二次函数f(x)=ax²+bx+c恒非负，且a<b，则            的最小值是____。

．已知函数f(x)=x²+bx的图象在点A(1，f(1))处的切线与直线3x-y+2=0平行，若数列的前n项和为S_n,则S₂₀₀₉的值为(    )

A．

B．

C．

D．

已知函数，且没有实数根，那么 的实根根数个数为（   ）

A．0

B．1

C．2

D．4

若，则函数=                     

函数的值域是（  ）

A．

B．

C．

D．