高中数学二次剩余试题

函数f(x)＝ax²＋ax－1在R上恒满足f(x)<0，则a的取值范围是(　　)

A．a≤0	B．a<－4
C．－4<a<0	D．－4<a≤0

若函数y＝ax与y＝－在(0，＋∞)上都是减函数，则y＝ax²＋bx在(0，＋∞)上(　　)

A．单调递增	B．单调递减
C．先增后减	D．先减后增

函数的最大值为_________

设f(x)与g(x)是定义在同一区间[a，b]上的两个函数，若函数y＝f(x)－g(x)在x∈[a，b]上有两个不同的零点，则称f(x)和g(x)在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”．若f(x)＝x²－3x＋4与g(x)＝2x＋m在[0,3]上是“关联函数”，则m的取值范围为________．

若函数f(x)＝x²－ax－a在区间[0,2]上的最大值为1，则实数a等于________．

已知函数.
(1)求不等式的解集;
(2)设,其中R,求在区间上的最小值.

已知函数 $f\left(x\right)=\{\begin{array}{c}{2}^x,x>0\\ x+1,x\le 0\end{array}$．若 $f\left(a\right)=f\left(1\right)=0$，则实数 $a$的值等于（        ）

A．

﹣3

B．

﹣1

C．

1

D．

3

抛物线与轴的两个交点的横坐标分别为1和3，则不等式的解集是                    ．

若不等式对任意的，恒成立，则实数的取值范围是      ．

已知中心在原点，焦点在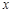轴上的椭圆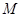的离心率为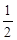，椭圆上异于长轴顶点的任意点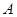与左右两焦点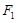、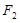构成的三角形中面积的最大值为.
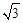（1）求椭圆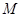的标准方程；
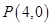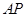（2）已知点，连接与椭圆的另一交点记为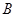，若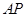与椭圆相切时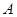、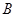不重合，连接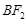与椭圆的另一交点记为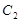，求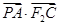的取值范围.

已知a、b为非零向量，，若，当且仅当时，取得最小值，则向量a、b的夹角为___________.

关于的不等式的解集为，且，则（　　）

A．

B．

C．

D．

已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x²+2ax+1+a²,g(x)=x-+.
(1)求函数f(x)的最小值.
(2)对于∀x₁,x₂∈[0,2],f(x₁)>g(x₂)恒成立,求实数a的取值范围.

某公司在甲、乙两地销售一种品牌车,利润(单位：万元)分别为L₁=5.06x-0.15x²和L₂=2x,其中x为销售量(单位：辆).若该公司在这两地共销售15辆车,则能获得的最大利润为(　　)

A．45.606万元	B．45.6万元
C．45.56万元	D．45.51万元

已知二次函数的二次项系数为，且不等式的解集为（1，3）．
⑴若方程有两个相等实数根，求的解析式．
⑵若的最大值为正数，求实数的取值范围．