(本小题满分14分)
椭圆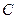 :
: 的离心率为
的离心率为 ,长
,长 轴端点与短轴端点间的距离为
轴端点与短轴端点间的距离为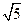 。
。
(I)求椭圆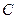 的方程;
的方程;
(II)设过点
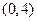
 的直线
的直线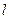 与椭圆
与椭圆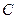 交于
交于 两点,
两点,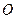 为坐标原点,若
为坐标原点,若
为直角三角形,求直线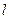 的斜率。
的斜率。
(本小题满分13分)
过圆 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于点D(9,0)的对称点为E,O为坐标原点,将线段OP绕原点O依逆时针方向旋转90°后,所得线段为OF,求|EF|的取值范围.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆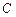 :
: (
( ),其左、右焦点分别为
),其左、右焦点分别为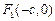 、
、 ,且
,且 、
、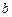 、
、 成等比数列.
成等比数列.
(1)求 的值.
的值.
(2)若椭圆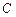 的上顶点、右顶点分别为
的上顶点、右顶点分别为 、
、 ,求证:
,求证: .
.
(3)若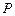 为椭圆
为椭圆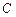 上的任意一点,是否存在过点
上的任意一点,是否存在过点 、
、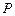 的直线
的直线 ,使
,使 与
与 轴的交点
轴的交点 满足
满足 ?若存在,求直线
?若存在,求直线 的斜率
的斜率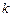 ;若不存在,请说明理由.
;若不存在,请说明理由.
如图,过点 作垂直于
作垂直于 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,又过点
,又过点 作
作 轴的平行线交
轴的平行线交 轴于点
轴于点 ,记点
,记点 关于直线
关于直线 的对称点为
的对称点为 ;……;依此类推.若数列
;……;依此类推.若数列 的各项分别为点列
的各项分别为点列 的横坐标,且
的横坐标,且 ,则
,则 .
.
(本小题满分14分)
已知椭圆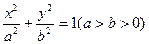 的左、右焦点分别为F1、F2,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形。
的左、右焦点分别为F1、F2,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形。
(1)求椭圆的方程;
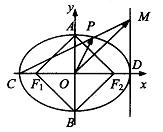
(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P。证明: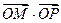 为定值。
为定值。
(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由。
(本小题满分13分)
设椭圆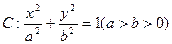 的离心率
的离心率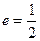 ,右焦点到直线
,右焦点到直线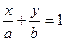 的距离
的距离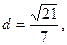
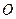 为坐标原点.
为坐标原点.
(I)求椭圆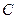 的方程;
的方程;
(II)过点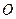 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆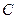 分别交于
分别交于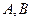 两点,证明点
两点,证明点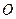 到直
到直
线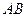 的距离为定值,并求弦
的距离为定值,并求弦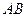 长度的最小值.
长度的最小值.
和
的极坐标方程分别为
.
(Ⅰ)把
和
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过
交点的直线的直角坐标方程.
如图,已知 是 的切线, 为切点, 是⊙O的割线,与 交于 、 两点,圆心 在 的内部,点 是 的中点.

(Ⅰ)证明
四点共圆;
(Ⅱ)求
的大小.
抛物线 的焦点为 ,准线为 ,经过 且斜率为 的直线与抛物线在 轴上方的部分相交于点 ,垂足为 ,则 的面积是
| A. | 4 | B. | C. | D. | 8 |
设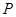 是曲线
是曲线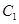 上的任一点,
上的任一点, 是曲线
是曲线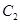 上的任一点,称
上的任一点,称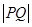 的最小值为曲线
的最小值为曲线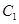 与曲线
与曲线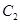 的距离.
的距离.
(1)求曲线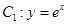 与直线
与直线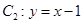 的距离;
的距离;
(2)设曲线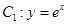 与直线
与直线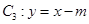 (
(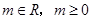 )的距离为
)的距离为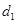 ,直线
,直线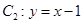 与直线
与直线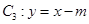 的距离为
的距离为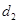 ,求
,求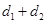 的最小值.
的最小值.
试题篮
()